Puede que no lo reconozcamos, pero la densidad forma parte de nuestra cotidianidad: en las mezclas de ingredientes de cocina, la separación entre el agua y el aceite, el vuelo de los aviones y la flotabilidad de los barcos. Gracias a la densidad, las placas de hielo flotan encima del agua y no se hunden. Lo cual evita que los fondos marinos se congelen.
Por ejemplo, si vamos a comprar un colchón debemos prestar especial atención a esta magnitud. Los colchones suelen clasificarse, entre tantas cosas, por su densidad. Los más densos son más duros y pesados, mientras que sus opuestos se curvan con mayor suavidad.
Los materiales de baja densidad suelen ser porosos y contener mayor separación entre sus fibras. Esta condición los hace ideales para ser usados como aislantes sonoros o térmicos. También les permite poseer mayor flotabilidad en el agua. Comprobar la densidad absoluta es bastante sencillo y lo puedes hacer empleando la siguiente metodología.
La densidad absoluta (ρ) de un material es la relación entre su masa (m) y su volumen (V). Es decir, la masa dividida por el volumen. El material considerado puede ser un líquido, un sólido o un gas. La unidad de medida de la densidad es el kilogramo por metro cúbico (kg/m³); aunque en el uso diario se suele expresar en kilogramos por litro (kg/litro), gramos por mililitros (g/ml) o también en gramos por centímetro cúbico (g/cm³).
ρ = m / V

Un dato curioso asociado a la densidad se asocia con la expresión eureka. Según cuenta la historia, el rey Hierrón II le dio a Arquímedes la tarea de comprobar si un orfebre, encargado de fabricar una corona de oro para los dioses, había sustraído parte del oro entregado como materia prima para crear la joya.
La forma común de realizar esta comprobación en la época hubiera sido derretir la corona y fundirla en un molde cúbico que permitiera calcular su volumen. Pero, obviamente, no querían destruirla.
Entonces Arquímedes, al sumergirse en una bañera con agua, notó algo que le ayudaría a resolver el problema. Midiendo el desplazamiento del agua al sumergir la corona, podría saber si el volumen era igual o no al de la pieza de materia prima entregada al orfebre.
La historia también cuenta que Arquímedes comenzó a gritar «¡eureka!, ¡eureka!», mientras corría desnudo por la calle feliz por haber encontrado una solución al problema. De ahí que se asocie el término eureka con un momento de brillantez al encontrar la solución a un problema.
Calcular la densidad de un objeto (sólido)
La fórmula de densidad es bastante sencilla (ρ = m / V) siempre que contemos con los datos de masa y volumen. Pero, ¿qué sucede cuando nos vemos en la situación de Arquímedes y tenemos un objeto cuya forma es bastante asimétrica y no nos permite calcular su volumen de manera sencilla?
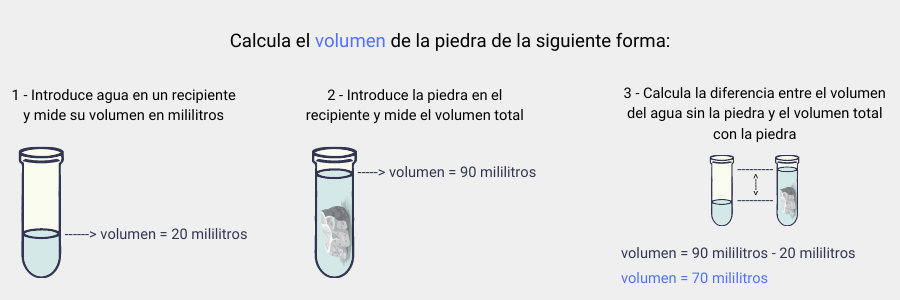
Para ello, necesitamos medir la masa del objeto con la ayuda de una báscula. Si es un objeto de dimensiones pequeñas, te recomendamos utilizar el gramo como unidad de medida. El cálculo del volumen podemos hacerlo basado en el principio de Arquímides. Mediremos la cantidad de agua en un recipiente y luego calcularemos la cantidad que se desplaza al introducir el objeto. La cantidad de agua desplazada coincidirá con el volumen del objeto.
Dicho así puede que no te quede claro, pero con un ejemplo lo comprenderás mejor. Supongamos que quieres calcular la densidad de una piedra. Deberás seguir los siguientes pasos.



Densidad de los metales
Aunque puedes emplear las fórmulas anteriores para calcular la densidad de un metal, también puedes ahorrarte estos cálculos y acudir a las densidades conocidas. A continuación compartimos un listado con los más comunes.
Metal - Densidad (kg/dm³)
Aluminio – 2.69 kg/dm³
Cobalto – 8.9 kg/dm³
Cobre – 8.9 kg/dm³
Cromo – 7.1 kg/dm³
Estaño – 7.28 kg/dm³
Magnesio – 1.74 kg/dm³
Plomo – 11.34 kg/dm³
Titanio – 4.45 kg/dm³
Zinc – 7.13 kg/dm³
Densidad de una esfera <h3>
Para el cálculo de la densidad de una esfera realizamos el mismo procedimiento de ejemplos anteriores (ρ = m / V). Con la condición de que el volumen de la esfera se puede calcular de manera directa, pues conocemos su fórmula y no es compleja.
V(esfera) = (4* π * r³) / 3



Calcular la densidad de una sustancia (líquida)
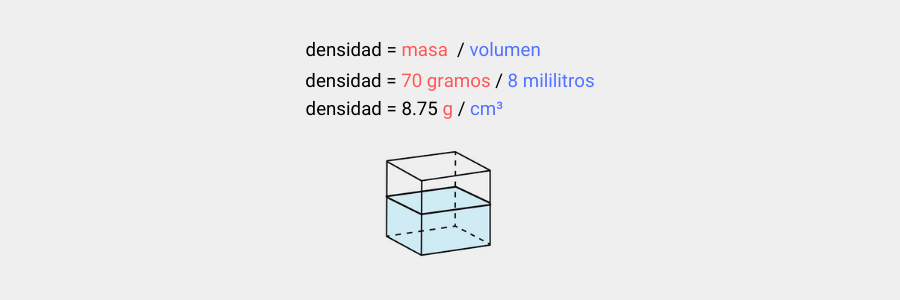
Aunque tomemos en cuenta sustancias líquidas, la densidad continúa manteniendo su fórmula básica (ρ = m / V). Con lo cual, lo que varía es la fórmula para calcular la masa y el volumen de la sustancia (en los casos en que no tenemos esos datos).
La masa la podemos calcular también empleando una báscula. Tengamos en cuenta que, antes de calcular la masa de la sustancia, debemos calcular la del recipiente en el que la colocaremos. Para luego restarle la masa del recipiente.
Aquí cada uno de los pasos:


Algunas densidades conocidas de sustancias líquidas
Si deseas ahorrar tiempo y acceder fácilmente al valor de la densidad de una sustancia líquida, te presentamos un listado de las más utilizadas.
Sustancia - Densidad (kg/m³)
Aceite - 920.02
Agua - 1 000.02
Agua de mar - 1 027.0202
Alcohol - 780.902
Gasolina - 683
Sangre 1060 - 1 088
¿Cómo calcular? es una columna para contribuir a la educación ciudadana en temas de datos, estadística y matemática práctica en la vida cotidiana. Puedes leer aquí todos los textos publicados.










Comentarios
En este sitio moderamos los comentarios. Si quiere conocer más detalles, lea nuestra Política de Privacidad.
Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *
Rafael